Comparing Tourist Preferences in Asia and Europe¶
Sam Childs and Vasanth Rajasekaran
Table of Contents¶
- Introduction
- Loading and Cleaning Data
- Initial Analysis
- Investigating Relationships
- K-Means Clustering
- Predicting Ratings
- Applications
- Conclusion
Part 1: Introduction¶
Vasanth and I (Sam Childs) will be working together on the final tutorial for this class. We decided that we wanted to work with some sort of data that had to do with travel/global activities. We were both interested in finding how behavior could be different in different parts of the world. Also, we were thinking of the times before covid and got a little nostalgic. We identified a dataset from UC Irvine which includes review data from travelers on Google Reviews. It is called “Travel Review Rating Dataset”, and it is found in the university’s Machine Learning Repository. We also found a dataset from TripAdvisor that had data on travelers from Asia from the same repository. We are interested in asking questions about whether average user feedback for a specific type of attraction yields insights into other kinds of attractions. Perhaps certain attraction classes have overlapping sets of fans, or perhaps another attraction class is highly polarizing. We are also wondering about frequency of reviews by attraction class. Perhaps few people who enjoy attraction type A try attraction type B, but the few that do really enjoy the experience. Insights into how markets for travel entertainment clear inefficiently would be of great value to tourism boards and travel companies.
Initial Questions¶
- Does a reviewer's affinity for certain attraction types in turn show affinity for others?
- How does tourist affinity differ between Asia and Europe?
- Can we predict how much a user will like a certain type of attraction based on their other reviews?
Collaboration Plan¶
To facilitate collaboration, we set up a private Github repository to share workbooks and data. We will ensure that each commit to the Git repo will include thorough comments documenting the changes. We will meet over the phone weekly to update each other on our progress, or more frequently as necessary to facilitate deadlines. Included in these meetings will be discussions about how to resolve merges/conflicts as they arise during our work.
Link to dataset: https://archive.ics.uci.edu/ml/datasets/Tarvel+Review+Ratings
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
#The names list for the data set that is given on the data source website
googleColumns=[ 'Unique user id '
,'Average ratings on churches'
,'Average ratings on resorts'
,'Average ratings on beaches'
,'Average ratings on parks'
,'Average ratings on theatres'
,'Average ratings on museums'
,'Average ratings on malls'
,'Average ratings on zoo'
,'Average ratings on restaurants'
,'Average ratings on pubs/bars'
,'Average ratings on local services'
,'Average ratings on burger/pizza shops'
,'Average ratings on hotels/other lodgings'
,'Average ratings on juice bars'
,'Average ratings on art galleries'
,'Average ratings on dance clubs'
,'Average ratings on swimming pools'
,'Average ratings on gyms'
,'Average ratings on bakeries'
,'Average ratings on beauty & spas'
,'Average ratings on cafes'
,'Average ratings on view points'
,'Average ratings on monuments'
,'Average ratings on gardens']
googleData = pd.read_csv('./data/google_review_ratings.csv', header = 0, names=googleColumns, index_col=False)
# reads ratings CSV into pandas using header 0 and names from the list above
googleData = googleData.set_index('Unique user id ') # sets USER ID Column to index
googleData = googleData.drop('Average ratings on local services',axis=1) # This column is corrupted and we decided to remove it
googleData # shows dataframe
Cleaning Google reviews data¶
The travel data set was a relatively simple to import and format correctly. The first step was to define the column names as per the UCI ML website, there is a large list of names at the top. The second step was to read the csv using pandas. For this we set the heading to zero to cut out a row of vauge names (category 1, category, etc.) that come with the data set. We also had to set the index_col to false inorder to make the columns line up with the data. The data is now indexed correctly by user with specific categories for names. We decided to remove the "Local Services" column because it had several corrupted values. It does not exist in the Tripadvisor dataset, so its removal does not affect our analysis.
Tripadvisor Data¶
We found an additional dataset from Tripadvisor for average review score on various categories from travelers in Asia. Although not all of the attributes match between the datasets, we do have some overlapping that will allow for some comparisons between the two. Important to note: The ratings on trip advisor are 0-4 rather than the 1-5 found on the google data (we account for this in our analysis)
TAColumns = [
'Unique user id',
'Average ratings on art galleries',
'Average ratings on dance clubs',
'Average ratings on juice bars',
'Average ratings on restaurants',
'Average ratings on museums',
'Average ratings on resorts',
'Average ratings on parks',
'Average ratings on beaches',
'Average ratings on theatres',
'Average ratings on religious institutions'
]
TAData = pd.read_csv('./data/tripadvisor_review.csv', header=0, names=TAColumns)
TAData = TAData.set_index('Unique user id')
TAData
Cleaning our Tripadvisor Data:¶
The travel data set was also relatively simple to import and format correctly. The first step was to define the column names as per the documentation from UCI Machine Learning Repository. The second step was to read the csv using pandas. For this we set the heading to zero to cut out a row of vauge names (category 1, category, etc.) that come with the data set. We also had to set the index_col to false in order to make the columns line up with the data. The data is now indexed correctly by user with specific categories for names. (Note that these unique user ID's are not the same users as the other data set even though many values will appear in both the data sets).
Part 3: Exploring our Datasets and Initial Analysis¶
To explore our data, we decided to first check some measures of central tendency to better understand what attraction types were popular from a high level.
Average Ratings per Category¶
First we looked at the data from Asia (Tripadvisor) and created a chart to show the differences in rating between the different categories
# Rank the categories by highest average:
TAAvg = TAData.mean(axis=0).round(2)
print(TAAvg.sort_values(ascending = False))
TAAvg.plot.bar()
From this chart we can see that parks and beachs have the highest average rating, along with religious institutions.
Next lets look at the Europe data (Google)
# Rank the categories by highest average:
avg = googleData.mean(axis = 0).round(2)
print(avg.sort_values(ascending = False))
avg.plot.bar() # This dataset has a fairly wide range of average category scores
From the chart above we see that there are many types of attractions that all have high and similar ratings to one another. Particularly we can see that malls and resturants are two of the highest.
# Figure out the ratio of reviews above 1 (2 is a rating of average).
mostLike = []
for col in TAColumns[1:]:
mask = (TAData[col] >= 1)
try:
ratio = (mask.value_counts()[True] / (mask.value_counts()[False]+mask.value_counts()[True]))*100
print(str(ratio.round(2)) + '% users considered near average or above for', col)
if ratio > 50:
mostLike.append(col)
except:
print('100% users considered near average or above for', col)
mostLike.append(col)
print('--------------------------------------')
print('Attractions that most people think are near average or above:')
TAData[mostLike].head()
This table shows the ratios of ratings above 1 per category. A rating of 2 is considered average for a rating on trip advisor, thus we can which categories users thought were near or above average. We see that tourists in Asia seem to like resorts, parks, beaches, and religious sites across the board. For the other categories, most users seemed to deem them not up to average
We tried the same with the Google data but chose 2 as the baseline number since a 3 is considered average in Google reviews, below the resulting table.
mostLike = []
for col in googleData[1:]:
#print(col)
mask = (googleData[col] >= 2)
try:
ratio = (mask.value_counts()[True] / (mask.value_counts()[False]+mask.value_counts()[True]))*100
print(str(round(ratio,2)) + '% users gave near average or above for', col)
if ratio > 50:
mostLike.append(col)
except:
print('100% users considered near average or above for', col)
print('--------------------------------------')
print('Attractions that most people think are near average or above:')
googleData[mostLike].head()
This table shows the ratios of ratings above 1 per category. A rating of 2 is considered average for a rating on trip advisor, thus we can see which categories users thought were near or above average. From a glance, we see that parks, beaches, and theaters are popular. However, we can also see some attractions popular in Asia are not as popular in Europe, ex. dance clubs.
To reach a more direct analysis between the two datasets, we decided to isolate the categories common to both. Note: we add 1 to all TA data to make the scale 1-5 rather than 0-4 to match with the google data.
commonCategories =[
'Average ratings on art galleries',
'Average ratings on dance clubs',
'Average ratings on juice bars',
'Average ratings on restaurants',
'Average ratings on museums',
'Average ratings on resorts',
'Average ratings on parks',
'Average ratings on beaches',
'Average ratings on theatres'
]
taCopy = TAData.copy()
taCopy[commonCategories] += 1 # add one to all TA data to make the scales of google and TA match
a = googleData[commonCategories].mean()
b = taCopy[commonCategories].mean()
plt.figure(1)
plt.clf()
plt.bar(commonCategories,a, color = 'r', label='Google Data', alpha=.5)
plt.bar(commonCategories,b, color = 'b', label='Trip Advisor Data', alpha=.5)
plt.xticks(rotation= 30,ha="right")
plt.legend=True
plt.stack = False
plt.show()
Google Data in Red
Tripadvisor Data in Blue
The graph above compares the average ratings between the EU and Asia data in the common categories. We see that things like resturants and juice bars are higher rated in Europe while parks and beaches are rated higher in Asia. There seems to be more of an affinity for the outdoors in Asia
Part 4: Investigating Relationships¶
While these initial comparisons were interesting we wanted to check if there is any correlation between certain categories within the data sets
import json
import math
googleCor = {}
for i in googleData:
googleCor[i] = []
for j in googleData: # loop through google data
if i == j:
continue
if abs(googleData[i].corr(googleData[j])) > 0.5: # .5 is considered the baseline for correlation
googleCor[i].append((j,round(googleData[i].corr(googleData[j]), 4))) # if greater than .5 append
googleCor = {key:val for key, val in googleCor.items() if val != []} # get rid of attributes with no corr
pd.DataFrame(googleCor.values(), index=googleCor.keys()) # turn into a df
This table shows the correlations between average ratings greater than 50% for the Google Dataset. Some of these correlations are consistent with our intuition (ex: Restaurants + Bars, or Gyms + Pools) whereas some represent less obvious trends. The highest correlation between categories is between parks and theaters.
TACor = {}
for i in TAData:
TACor[i] = []
for j in TAData:
if i == j:
continue
if abs(TAData[i].corr(TAData[j])) > 0.5:
TACor[i].append((j,round(TAData[i].corr(TAData[j]), 4)))
TACor = {key:val for key, val in TACor.items() if val != []}
pd.DataFrame(TACor.values(), index=TACor.keys())
This table shows the correlations between average ratings greater than 50% for the Tripadvisor Dataset. Similarly to the google dataset, some of the correlations are intuitive, whereas others are somewhat surprising. For example, the strong inverse correlation between parks and religious institutions.
Part 5: Finding Clusters in our Data¶
To address our question of whether certain affinities are related to each other, we decided to run a clustering algorithm on our copies of our datasets that only contained the common elements. We decided to use K-Means Clustering since it seemed the a solid way to explore whether we had clusters and what they are.
We used the Sklearn library to implement our model.
Google Data¶
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
new = googleData[commonCategories]
inertias = []
for i in range(1,10): # run the algo 1-10 to plot inertias
model = KMeans(n_clusters=i)
model.fit(new) # run mode for current k
inertias.append(model.inertia_)
plt.figure(figsize=(16,8))
plt.plot(range(1,10), inertias, 'bx-')
plt.xlabel('k')
plt.ylabel('inertias')
plt.title('The Elbow Method showing the optimal k for the Google Dataset')
plt.show()
To choose an optimal K Clusters, we decided to analyze inertia (sum of squared distances) and check where the "elbow" of our graph is. We arrive at an optimal K = 3.
Below we run our model and plot the results.
kmeans = KMeans(n_clusters=3) # set clusters = 3
kmeans.fit(new) # run model
clusterNames = kmeans.labels_
X = new
y = clusterNames
target_names = [0,1,2]
pca = PCA(n_components=2) # reduce dimesions of the data using PCA and LDA
X_r = pca.fit(X).transform(X)
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
plt.figure(figsize=(16,8))
colors = ['#ffa60a', '#880000', '#0a0054',]
for color, i, target_name in zip(colors, range(0,4), target_names): # plot clusters
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.5,
label=target_name)
plt.title('Google dataset clusters using PCA')
plt.show()
To visualize our clusters, we needed to reduce the dimensionality of our data. To achieve this, we applied Principal Component Analysis (PCA). We tried other methods, including Linear Discriminant Analysis, but the assumptions it uses to extract feature subspaces did not produce compelling visualizations of our clusters. We found that LDA (Below)'s feature subspaces did not coincide with the cluters identified by the K-Means algorithm. The result is an uncompelling visualization, so we decided to stick with PCA.
plt.figure(figsize=(16,8))
for color, i, target_name in zip(colors, range(0,4), target_names):
plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.5, color=color,
label=target_name)
plt.title('Google dataset clusters using LDA')
plt.show()
One problem we ran into while visualizing our clusters has to do with the non-deterministic nature of the K-Means algo. Because the algorithm randomizes the initial centroids, the resulting clusters are not exactly the same between iterations. As a result, our visuals and the colors corresponding to clusters moved around between iterations.
Below, we loop through the our data and split the points based on their clusters and show the average ratings to paint a picture for users in each cluster.
people = list(clusterNames)
zero = []
one = []
two = []
for i in range(len(people)):
if people[i] == 0:
zero.append(i)
elif people[i] == 1:
one.append(i)
else:
two.append(i)
new.iloc[zero].mean().round(4) # Yellow cluster
new.iloc[one].mean().round(4) # Red cluster
new.iloc[two].mean().round(4) # Blue cluster
Because we are in an unsupervised learning environment, at some point, a human with domain expertise will need to intervene to label the clusters.
So a data analyst at a travel company might look at the mean review scores for these clusters and assign labels to help communicate the insight to management.
- Strong preference for Theaters, Parks, and Museums. "The Cultured Urbanite"
- Mostly low scores across the board. "The Pessimist"
- Loves art galleries. "The Art Connaisseur"
These kinds of qualitative labels for clusters of user data are more compelling with the introduction of psychographic features.
Tripadvisor Data¶
We applied the same methodology to determine the optimal number of clusters for the dataset from Tripadvisor. Ultimately, we arrived at 2 clusters.
TANew = TAData[commonCategories] + 1 # to give the data the same scale as the google data
inertias = []
for i in range(1,10):
model = KMeans(n_clusters=i)
model.fit(TANew)
inertias.append(model.inertia_)
plt.figure(figsize=(16,8))
plt.plot(range(1,10), inertias, 'bx-')
plt.xlabel('k')
plt.ylabel('inertias')
plt.title('The Elbow Method showing the optimal k for Tripadvisor')
plt.show()
kmeans = KMeans(n_clusters=2)
kmeans.fit(TANew)
clusterNames = kmeans.labels_
X = TANew
y = clusterNames
target_names = [0,1]
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
plt.figure(figsize=(16,8))
colors = ['#ffa60a', '#880000', '#0a0054',]
for color, i, target_name in zip(colors, range(0,4), target_names):
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.5,
label=target_name)
plt.title('PCA of Tripadvisor Dataset')
plt.show()
people = list(clusterNames)
zero = []
one = []
for i in range(len(people)):
if people[i] == 0:
zero.append(i)
elif people[i] == 1:
one.append(i)
TANew.iloc[zero].mean() #Yellow Cluster
TANew.iloc[one].mean() # Red Cluster
After applying the same methods to the trip advisor data, we saw two clusters that are relativly similar. This data might not have any separable features, and the relatively small scale of the data set could also be limiting our clustering efforts. For these reasons, we did not attempt to assign qualitative labels to these clusters like we did in the Google Dataset.
Part 6: Predicting Ratings¶
Based on the clusters we found, we wondered if we could predict a user's rating for a attraction based on their other ratings. To answer this question we decided to use the K-Closest neighbors algorithm and test a few example users to see if we could predict their ratings.
Below we set up a sample user whos ratings were similar to an average user from the cluster that loves art galleries.
from sklearn.feature_extraction import DictVectorizer
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score
kNData = googleData[commonCategories]
features = [ # set up features
'Average ratings on art galleries',
'Average ratings on dance clubs',
'Average ratings on juice bars',
'Average ratings on museums',
'Average ratings on resorts',
'Average ratings on parks',
'Average ratings on beaches',
'Average ratings on theatres'
]
xTrainDict = kNData[features].to_dict(orient='records') # defining training data
yTrain = kNData['Average ratings on restaurants'] # what we want to find out
vec = DictVectorizer(sparse=False)
scaler = StandardScaler()
average = 0
MAE = {}
high = (0,99)
for i in range(1,20):
model = KNeighborsRegressor(n_neighbors=i)
pipeline = Pipeline([("vectorizer", vec), ("scaler", scaler), ("fit", model)])
scores = -cross_val_score(pipeline, xTrainDict, yTrain, cv=5, scoring="neg_mean_absolute_error") # run pipeline with 5 folds
MAE[i]=scores.mean() # find mean to plot easily
if scores.mean() < high[1]: #store value if lower
high = (i,scores.mean())
print(high)
plt.plot(*zip(*sorted(MAE.items()))) # plot all items
plt.show()
To create a model that generalizes well to new data, we conducted a k-nearest-neighbors regression with 5-fold crossvalidation. We tested K's 1-20 and found that the optimal K to minimize MAE was 2. However the MAE is somewhat high at 0.49 meaning that on average our prediciction is off by about 10% of the range of possible scores. This leads to some predictability, but a different model could improve upon this result.
TripAdvisor Data¶
We run the same type of model for the TA data
TAKData = TAData[commonCategories] +1
features = [
'Average ratings on art galleries',
'Average ratings on dance clubs',
'Average ratings on juice bars',
'Average ratings on museums',
'Average ratings on resorts',
'Average ratings on parks',
'Average ratings on beaches',
'Average ratings on theatres'
]
xTrainDict = TAKData[features].to_dict(orient='records') # defining training data
yTrain = TAKData['Average ratings on restaurants'] # what we want to find out
vec = DictVectorizer(sparse=False)
scaler = StandardScaler()
MAE = {}
high = (0,99)
for i in range(1,50):
model = KNeighborsRegressor(n_neighbors=i)
pipeline = Pipeline([("vectorizer", vec), ("scaler", scaler), ("fit", model)])
scores = -cross_val_score(pipeline, xTrainDict, yTrain, cv=5, scoring="neg_mean_absolute_error") # run pipeline with 5 folds
MAE[i]=scores.mean() # find mean to plot easily
if scores.mean() < high[1]: #store value if lower
high = (i,scores.mean())
print(high)
plt.plot(*zip(*sorted(MAE.items()))) # plot all items
plt.show()
From the graph above we see the optimal k is 12 with a MAE of 0.12. From the MAE we can see our model is pretty accurate with only 2.4% error on average. This model is a lot more predictive, and because we used cross validation we can be somewhat confident in the model's ability to generalize.
Part 7: Applications of our work¶
A predictive model has many applications within the monetization of a review platform. For example, after you leave a review for the restaurant where you just ate a meal, the app could recommend a place to get desert. To illustrate this idea, we created a simple mockup of how this interface could be implemented. Note: image may not show due to how github pages is handling the html
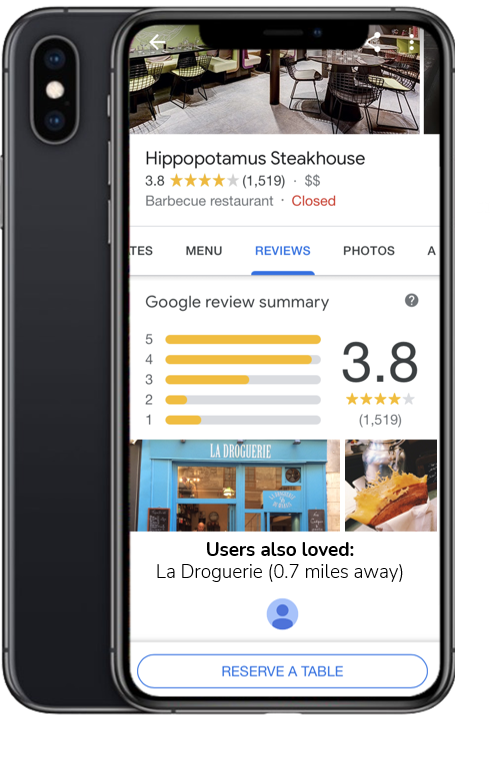
Understanding who is more likely to respond to an app's recommendations means advertising space can be allocated more efficiently.
Part 8: Conclusion¶
To conclude our research, we will review the answers to our initial questions:
1. Does a reviewer's affinity for certain attraction types in turn show affinity for others?¶
Yes, we can see stable clusters in the Europe Google Reviews data which indicates that in some cases, affinity for one attraction type is associated with an affinity (or lack thereof) for others. The lack of large differences in clusters in the Asia data means that for that population, affinity between different categories is less separable.
2. How does tourist affinity differ between Asia and Europe?¶
Because we have two different sets of clusters, and one of them isn't really distinguishable, we conclude that the two populations experience affinity differently. There are many confounding variables which could explain this phenomena. For example, the two different websites might attract different users, Google's inclusion of more categories might lead to different review outcomes, or the kinds of people who travel to each continent might be different psychographically. Without additional features in our data, we cannot fully understand the ways in which these datasets differ.
3. Can we predict how much a user will like a certain type of attraction based on their other reviews?¶
To an extent yes. While the Europe data set has an error rate of about 10% on average, while the Asia data set has an error rate of about 2.4%. We believe that more data would improve the confidence in our model's ability to generalize, although the use of crossvalidation proves that we are not overfitting.
Thank you for taking the time to learn more about our experiment. We hope you found it interesting!